C# Technique: Figure Out All Permutations Of A String

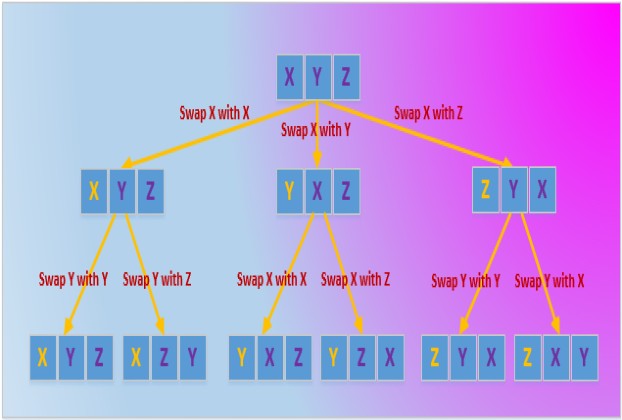
A Permutation is a re-arrangement of the elements of an ordered list such that each element in the list assumes every position in the list one by one. A string of length n has n! permutation. Putting it simple, a permutation of a string ABC will be all possible combinations of the characters ABC. There will be 3! that is, 3.2.1 = 6 possible combinations which are ABC, ACB, BAC, BCA, CAB, and CBA.

Given a string “ABCDE”, here’s a code example of how we achieve permutations of the string. Remember this code is completely flexible and you can use a string of any length to get all possible combinations of the characters from it. This is just a matter of swapping characters in an orderly manner. For instance, we’ll first swap 1st character and then permute the rest of the characters. For this purpose we use permute() function recursively.

        public static int abc = 0;

        static void Main(string[] args)
        {
            String str = "ABCDE";
            int n = str.Length;

	    /* Start permuation from the entire string, then within permute() keep calling itself recursively for the rest of the strings. */
            permute(str, 0, n - 1);	
        }

        private static void permute(String str, int l, int r)
        {
            if (l == r)
            {
                abc++; 
                System.Diagnostics.Debug.WriteLine(abc.ToString() + "- " + str);
            }
            else
            {
                for (int i = l; i <= r; i++)
                {
                    str = swap(str, l, i);
                    permute(str, l + 1, r);
                    str = swap(str, l, i);
                }
            }
        }

        public static String swap(String a, int i, int j)
        {
            char temp;
            char[] charArray = a.ToCharArray();
            temp = charArray[i];
            charArray[i] = charArray[j];
            charArray[j] = temp;
            string s = new string(charArray);
            return s;
        }